Integrali
Introduzione
1. Integrale Definito (e` un numero!)
2. Funzione Integrale (e` una funzione!)
3. Funzione Primitiva o Integrale Indefinito
4. Teorema Fondamentale del Calcolo
Conclusioni
Initialization (Evaluate this group of cells before proceeding!)
Introduzione
Per una funzione f(x) su un intervallo [a, b] desidero determinare un numero che rappresenti l' "area racchiusa dal grafico della funzione". Come posso calcolarlo? Per mezzo di un passaggio al limite!
![[Graphics:HTMLFiles/index_11.gif]](HTMLFiles/index_11.gif)
In figura: funzione f(x) = 1 - 2^(-x^2), intervallo [0, 4]; approssimazione ottenuta dividendo l'intervallo in n = 20 parti e sommando le aree dei rettangoli, ciascuno di base (b - a)/n. Aumentando il numero n si puo` ottenere una migliore approssimazione.
Un esempio
Nello stesso esempio, al variare del numero n di rettangoli da 2 a 25:
In[56]:=
RiemannSumMovie[1 - 2^(-x^2), {x, 0, 4}, {2, 25}];
Nello stesso esempio, per n=100:
In[57]:=
RiemannSumMovie[1 - 2^(-x^2), {x, 0, 4}, 100];
Integrale definito
Per ogni funzione continua, al limite per n → ∞, la somma delle aree dei rettangoli converge verso un numero che viene chiamato:
"integrale definito della funzione f(x) sull'intervallo [a, b]".
In simboli, definiamo: 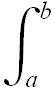 f(x)dx ≡
f(x)dx ≡
| lim |
| n→∞ |
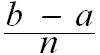
![Underoverscript[∑, i = 1, arg3]](HTMLFiles/index_49.gif) f(a + i
f(a + i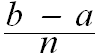 ) =
) =| lim |
| n→∞ |
![Underoverscript[∑, i = 1, arg3]](HTMLFiles/index_51.gif) f(a+iΔx)
f(a+iΔx)In[1]:=
f[x_] := 1-2^(-x^2); a = 0; b = 4; n = 10;
N[(b-a)/n Sum[f[a + i (b-a)/n], {i, 0, n - 1}]]
Out[2]=
![]()
Integrale definito: segno
L'integrale ha contributi negativi dagli intervalli in cui la funzione f(x) assume valori negativi
![[Graphics:HTMLFiles/index_58.gif]](HTMLFiles/index_58.gif)
Inoltre il segno cambia se si inverte l'ordine degli estremi di integrazione ([a, b] con b < a anziche` b > a)
Funzione Integrale
Ripetiamo il calcolo dell'integrale della funzione f(x') (pensata come funzione della variabile x') facendo variare l'estremo superiore x dell'intervallo di integrazione [a, x]: otteniamo una nuova funzione di x, che chiamiamo "funzione integrale" F(x)
F(x) ≡ 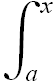 f(x')dx'
f(x')dx'
Un esempio:
In[11]:=
?AreaAccumulationMovie
In[12]:=
Clear[g, x]
In[13]:=
g[x_] := (x-2)^2(1.3 + 3.5x - 4.95x^2 + 2x^3 - 0.25x^4);
AreaAccumulationMovie[g[x], {x, 0, 4}, 10]
Funzione Primitiva o Integrale Indefinito
Data una funzione f(x), la funzione F(x) e` una "funzione primitiva di f(x)" se la sua derivata coincide con f(x)
F'(x) ≡ 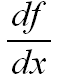 = f(x)
= f(x)
Se F(x) e` una primitiva di f(x), anche G(x) = F(x) + C, con C costante, e` una primitiva di f(x)
La funzione primitiva viene anche chiamata integrale indefinito, per il quale si usa anche la notazione di integrale senza estremi di integrazione:
![]() f(x)dx
f(x)dx
Teorema Fondamentale
Primo passo: la funzione integrale F(x) costruita con f(x) e` una primitiva di f(x). Verifichiamolo:
F'(x) ≡
| lim |
| Δx→0 |
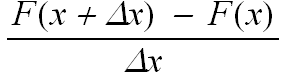 =
= 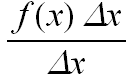 = f(x)
= f(x)![Underoverscript[∫, a, arg3]](HTMLFiles/index_91.gif) f(x')dx' -
f(x')dx' - ![Underoverscript[∫, x, arg3]](HTMLFiles/index_93.gif) f(x')dx' = f(x)Δx
f(x')dx' = f(x)ΔxIn[16]:=
FundamentalTheoremMovie[x^2, {x, 0, 4}]
Teorema fondamentale
Secondo passo: A questo punto e` facile verificare che per calcolare l'integrale definito di una funzione f(x) sull'intervallo [a, b] basta conoscere una qualsiasi primitiva F(x) e calcolare la differenza tra i valori che essa assume negli estremi a e b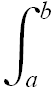 f(x)dx = F(b) - F(a)
f(x)dx = F(b) - F(a)
Dimostrazione: Sia F(x) una primitiva "fornitaci da qualcuno" (p.es tavole di integrali), e ![]() f(x')dx' la primitiva che sapremmo costruirci (se necessario numericamente) come funzione integrale: le due possono differire al piu`per una costante C:
f(x')dx' la primitiva che sapremmo costruirci (se necessario numericamente) come funzione integrale: le due possono differire al piu`per una costante C:
F(x) =![]() f(x')dx' + C
f(x')dx' + C
che pero` puo` essere determinata, considerando x=a e x=b :
F(b) =![]() f(x')dx' + C
f(x')dx' + C
F(a) =![]() f(x')dx' + C = 0 + C = C
f(x')dx' + C = 0 + C = C
da cui:
F(b) =![]() f(x')dx' + F(a)
f(x')dx' + F(a)
Avvertimenti
Abbiamo utilizzato piu` volte il significato geometrico dell'integrale definito come numero che rappresenta l'area racchiusa dal grafico della funzione. Implicitamente attribuiamo alle variabili x e y=f(x) dimensioni di lunghezza e all'integrale definito quello della misuradi una "superficie".
Attenzione! nelle applicazioni le due variabili x e y=f(x) possono essere a-dimensionali oppure avere dimensioni diverse, per esempio rispettivamente rappresentare un tempo ed una velocita` funzione del tempo: anche l'integrale definito sara` allora una quantita` dimensionale, da interpretare correttamente come grandezza fisica; in questo esempio, l'integrale corrispondera` ad uno spostamento, cioe` ad una "lunghezza" (prodotto di tempo e velocita`)
Conclusioni
In molte applicazioni e` utile calcolare l' "integrale definito" di una funzione (ad esempio: spostamento di un oggetto che si muova con velocita` variabile nel tempo), che e` un numero.
La "funzione integrale" (integrale con estremo superiore variabile) e` una primitiva della funzione integranda (cioe` ha derivata che coincide con la funzione integranda), ed in questo senso l'integrazione si puo` pensare come l'operazione inversa rispetto alla derivazione.
Nella pratica l'integrale definito viene spesso calcolato in modo approssimato, con metodi numerici che si basano sulla definizione (limite di una sommatoria).
Il Teorema Fondamentale offre un metodo alternativo e piu` rapido per calcolare l'integrale definito, ogni volta che sia gia` nota una primitiva F(x) della funzione integranda f(x), tramite la
![]() f(x)dx = F(b) - F(a)
f(x)dx = F(b) - F(a)
Created by Mathematica (November 16, 2004)