1/f Noise
1/f noise and flicker noises (i.e. the class of 1/f^alpha
noises - with 0.5 < alpha < 1.5) are as ubiquitous as they are
mysterious.
Several physical mechanisms to generate 1/f noise have been devised,
and
most of them try to obtain a broad, nearly flat distribution of
relaxation
times, which would then yield a 1/f spectrum. However they are
all
very specialized, and none of them addresses the question of the
apparent
universality of this noise, while they all fail in some respect. I have
shown that the power spectral density of a relaxing linear system
driven
by white noise is determined by the eigenvalue density of the linear
operator
associated to the system. I have also shown that the eigenvalue
densities
of linear operators that reasonably describe diffusion and transport
lead
to 1/f or flicker noise. I have been able to derive the Hooge
formula
for the spectrum of conductance fluctuations.
 Simulated white noise
Simulated white noise
 Simulated 1/f noise
Simulated 1/f noise
1/f
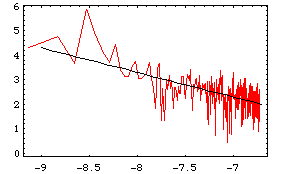
noise appears to be ubiquitous indeed: the following figure shows
the spectrum of the Wolf number for the period january 1953 - august
1995.
The Wolf number is an indicator of the solar activity
To
know more about 1/f noise you can read the paper
(sorry ... italian text only) that I wrote for "Le Scienze"
(italian
edition of Scientific American) and which appeared in the june 1996
issue,
or this review paper.
Last updated: 19 August 2002
 Simulated white noise
Simulated white noise
 Simulated white noise
Simulated white noise
 Simulated 1/f noise
Simulated 1/f noise
